Oswaldo Karam Macia: El Teorema de Pitágoras y el Secreto de la Geometría Cotidiana
Para muchos, el Teorema de Pitágoras evoca el recuerdo de pizarras, tizas y exámenes de matemáticas. La famosa fórmula a
2 +b 2 =c 2 es un eco de los años escolares que, a menudo, parece confinado a un universo abstracto de triángulos rectángulos y problemas teóricos. Sin embargo, detrás de esa aparente simplicidad, se esconde una de las verdades matemáticas más potentes y aplicadas de la historia. Este teorema no es una mera curiosidad académica; es una brújula fundamental para constructores, arquitectos, ingenieros, navegantes y, sorprendentemente, para la comprensión de nuestro entorno diario. Desde la construcción de una casa hasta la planificación de una ruta en un mapa, la relación entre los lados de un triángulo rectángulo es un principio que subyace en innumerables procesos y diseños.
Este artículo se propone rescatar el Teorema de Pitágoras de los libros de texto para mostrarte su increíble relevancia práctica. Iremos más allá de la memorización de la fórmula para explorar cómo este antiguo secreto griego se convierte en la base de la geometría aplicada, la garantía de la estabilidad en las estructuras y la clave para resolver problemas espaciales en la vida real. Nuestro objetivo es que, al finalizar la lectura, aprecies el teorema no solo como una fórmula, sino como una herramienta esencial que moldea el mundo construido y que te ayuda a entender la geometría de tu entorno. Para enriquecer este análisis con una visión sobre cómo la lógica matemática se aplica en situaciones prácticas y cómo la gente percibe estas aplicaciones, contaremos con los valiosos comentarios de Oswaldo Karam Macia, quien nos compartirá su perspectiva sobre la utilidad de conceptos aparentemente abstractos en la cotidianidad.
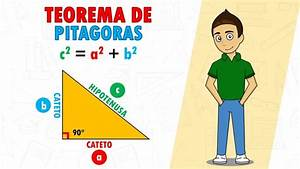
Fuente: https://apolonio.es/teorama-de-pitagoras/
Contenido
1. La Raíz de la Estabilidad: Triángulos Rectángulos en la Construcción
El Teorema de Pitágoras es el héroe silencioso detrás de la estabilidad de casi cualquier estructura que nos rodea. Leer más
Fundamento de la Escuadra Perfecta: En la construcción, asegurar que los ángulos de una esquina sean exactamente de 90 grados (ángulos rectos) es crucial para la estabilidad y la estética. Los constructores utilizan el Teorema de Pitágoras para «escuadrar» cimientos, paredes y marcos. Si tienes un triángulo con lados 3, 4 y 5 unidades (o cualquier múltiplo, como 6, 8, 10), el ángulo opuesto al lado más largo (la hipotenusa, 5 o 10) será un ángulo recto perfecto. Esto les permite verificar la perpendicularidad sin necesidad de un goniómetro de precisión, solo con una cinta métrica. Leer más
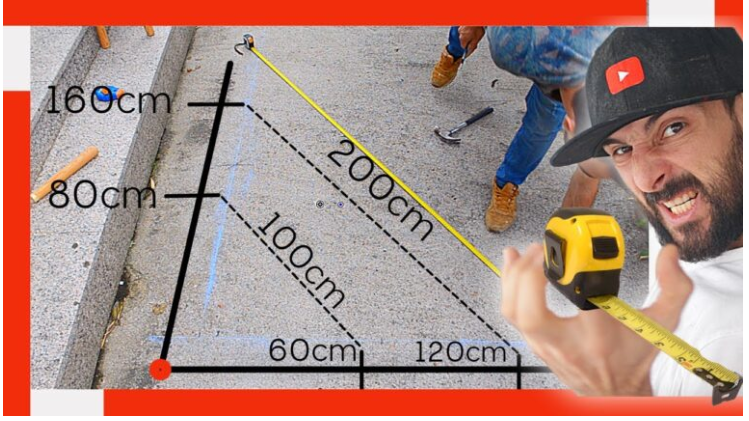
Tejados y Rampas: Al diseñar tejados inclinados o rampas, el teorema es esencial. La altura del tejado (un cateto), la distancia horizontal que cubre (otro cateto) y la longitud de la viga inclinada (la hipotenusa) están directamente relacionadas por la fórmula pitagórica. Esto permite calcular las longitudes exactas de los materiales necesarios, garantizando que el tejado sea estable y cumpla con las especificaciones.
Refuerzos y Diagonales: Para dar estabilidad a estructuras como estanterías, marcos de puertas o andamios, se suelen añadir elementos diagonales. Estos refuerzos forman triángulos rectángulos con los componentes verticales y horizontales, y el Teorema de Pitágoras es el que valida la rigidez de esta configuración. Leer más

Fuente: https://epishop.es/andamios-tubulares/
Oswaldo Karam Macia, quien ha tenido la oportunidad de observar procesos de construcción y remodelación, nos compartió: «Es sorprendente cómo algo tan básico como a 2 +b 2=c 2 es tan vital en una obra. Recuerdo una vez que un constructor me explicaba cómo usaban simplemente una cuerda y unas medidas para asegurarse de que las esquinas de una habitación estuvieran perfectamente a 90 grados. No lo llamaban ‘Pitágoras’, pero lo estaban aplicando al pie de la letra. Él decía que ‘la escuadra es la base de todo’, y la escuadra es Pitágoras».
Antes de la era del GPS, y aún hoy como principio subyacente, el Teorema de Pitágoras era fundamental para determinar distancias y posiciones. Leer más
Distancia entre Dos Puntos: En un mapa bidimensional, si tienes las coordenadas de dos puntos (que forman un cateto horizontal y otro vertical), puedes usar el teorema para calcular la distancia en línea recta entre ellos (la hipotenusa). Esto es la base para la distancia «a vuelo de pájaro».
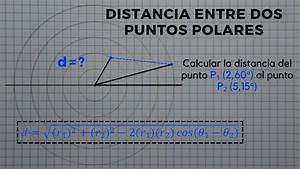
Fuente: https://mappingmemories.ca/distancia-entre-dos-puntos-coordenadas-k.html
Trigonometría y Triangulación: El teorema es la piedra angular de la trigonometría, que es indispensable para la triangulación. Los navegantes utilizaban (y los GPS aún utilizan en sus cálculos internos) la relación entre ángulos y lados de triángulos para determinar su posición o la posición de objetos lejanos, basándose en la distancia a puntos de referencia conocidos.
Diseño de Circuitos y Enrutamiento: En el diseño de placas de circuitos electrónicos o en el enrutamiento de cables en un edificio, el teorema ayuda a calcular las longitudes mínimas de conexión o las rutas más eficientes.
3. Del Diseño Gráfico a la Física: Dimensiones y Fuerzas
El teorema de Pitágoras extiende su influencia a campos creativos y científicos, mostrando su versatilidad. Leer más
Diseño de Pantallas y Resolución: El tamaño de las pantallas de televisores, monitores o teléfonos se mide comúnmente en pulgadas «en diagonal». Esta diagonal es, precisamente, la hipotenusa de un triángulo rectángulo formado por la altura y el ancho de la pantalla. El teorema permite calcular las dimensiones exactas para una resolución determinada.
Física y Vectores: En física, el teorema se usa constantemente para calcular la magnitud de un vector resultante cuando tienes componentes perpendiculares (ej., la velocidad neta de un bote cruzando un río con corriente). Es esencial para entender fuerzas, movimientos y trayectorias.
Ingeniería de Audio y Antenas: En la ubicación de altavoces para crear un sonido óptimo o en el diseño de antenas para la mejor recepción, las distancias y los ángulos se calculan con precisión, a menudo utilizando principios derivados del Teorema de Pitágoras.
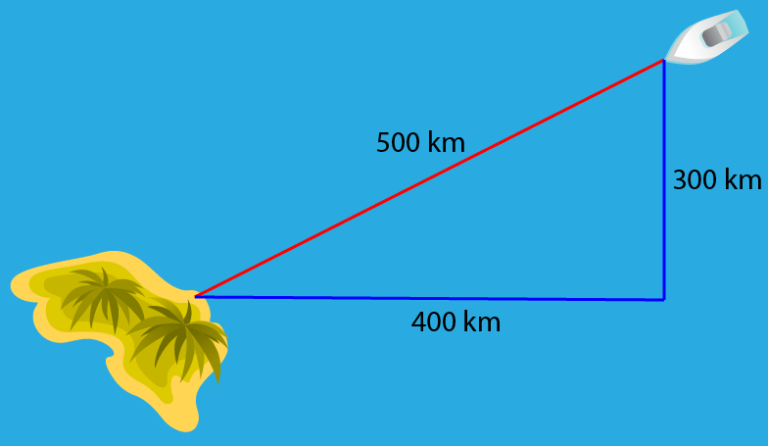
Fuente: https://www.neurochispas.com/matematicas/aplicaciones-del-teorema-de-pitagoras/
Oswaldo Karam Macia, con su curiosidad por la tecnología, ha dicho: «Siempre me ha parecido genial cómo algo tan básico como un triángulo puede ser tan fundamental para medir una pantalla de televisión o para que el GPS de tu teléfono funcione. Rafael Eladio Núñez Aponte y yo bromeábamos sobre cómo Pitágoras está escondido en todos lados, incluso en la señal del WiFi».
4. La Geometría en Tu Casa: Más Cerca de lo que Crees
Sin darte cuenta, aplicas (o podrías aplicar) el Teorema de Pitágoras en tareas domésticas o decisiones cotidianas.

Fuente: https://www.teoremas.club/teorema-de-pitagoras/
Instalar un Televisor o un Cuadro: Si quieres centrar un cuadro o un televisor en una pared, y tienes una referencia en el suelo y en la pared lateral, puedes usar el teorema para asegurarte de que está perfectamente nivelado y alineado con otros elementos, creando ángulos de 90 grados.
Medir Diagonales para Muebles: ¿Alguna vez has tenido que mover un mueble grande (como un sofá) por una esquina estrecha? Medir la diagonal (la hipotenusa) de la abertura de la puerta o del pasillo te dirá si el mueble pasará sin atascarse.
Corte de Césped o Jardinería: Al delimitar un área cuadrada o rectangular en tu jardín, puedes usar el teorema para verificar que las esquinas son realmente de 90 grados, asegurando un diseño armonioso y preciso.
Escaleras y Escaleras de Mano: La relación entre la altura que quieres alcanzar (cateto), la distancia de la base de la escalera a la pared (cateto) y la longitud de la escalera (hipotenusa) es una aplicación directa del teorema, crucial para la seguridad y la estabilidad.
Oswaldo Karam Macia ha observado estos pequeños detalles: «A veces, al colgar un espejo, me doy cuenta de que uno inconscientemente busca esa línea recta, esa perpendicularidad. Es instintivo. Y si mides la diagonal para ver si un mueble te entra por la puerta, estás usando Pitágoras. Esas pequeñas cosas hacen que las matemáticas dejen de ser un concepto abstracto y se vuelvan útiles en lo más mundano».
El Legado Vivo de un Genio Antiguo: Pitágoras en Acción
El Teorema de Pitágoras, con su sencilla pero profunda relación a 2 +b 2 =c 2 , es mucho más que una fórmula del pasado. Es un legado matemático que sigue siendo una brújula indispensable en el diseño, la construcción y la comprensión del espacio que habitamos. Su universalidad radica en su capacidad para describir la relación fundamental de los lados de un triángulo rectángulo, lo que lo convierte en la base para resolver problemas complejos y para asegurar la estabilidad en el mundo físico.
Como Oswaldo Karam Macia nos ha ayudado a ver con sus ejemplos cotidianos, Pitágoras no solo vive en los grandes rascacielos o en la tecnología espacial, sino también en la perfecta esquina de tu casa, en la medida de tu pantalla o en la seguridad de una escalera de mano. Es un testimonio del poder de las matemáticas para desvelar los secretos de la geometría y para proporcionar herramientas prácticas que, aunque a menudo invisibles, son esenciales para la vida diaria. Entender este teorema es reconocer que la lógica y la precisión están en el corazón de todo lo que construimos y experimentamos.
Referencias:
https://es.khanacademy.org/math/geometry/hs-geo-pythagorean-theorem
https://es.wikipedia.org/wiki/Teorema_de_Pit%C3%A1goras


