Oswaldo Karam Macia: Una Guía Sencilla para Entender la Trigonometría
La palabra trigonometría suele evocar recuerdos de clases de matemáticas complejas, llenas de fórmulas abstractas y ángulos incomprensibles. Sin embargo, detrás de esos términos técnicos se esconde una de las ramas más prácticas y fascinantes de las matemáticas. Desde la construcción de un rascacielos hasta la navegación por GPS, la trigonometría es una herramienta omnipresente que moldea nuestro mundo. Pero, ¿cómo podemos acercarnos a ella sin sentirnos abrumados? Esta guía tiene como objetivo desmitificar la trigonometría, mostrándola como lo que realmente es: el estudio de las relaciones entre los lados y los ángulos de los triángulos.
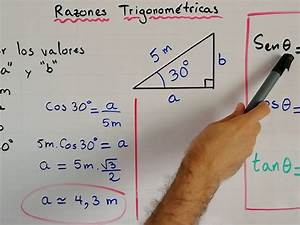
Fuente: https://quo.mx/estudios/10431/
Los Pilares Fundamentales: Seno, Coseno y Tangente
Para comenzar, necesitamos conocer a los tres mosqueteros de la trigonometría: seno (sin), coseno (cos) y tangente (tan). Estos tres conceptos son las funciones básicas que nos permiten calcular las relaciones en un triángulo rectángulo. Un triángulo rectángulo es aquel que tiene un ángulo de 90 grados. Dentro de él, tenemos tres elementos clave:
Hipotenusa: El lado más largo y el opuesto al ángulo recto. Leer más
Cateto Opuesto: El lado que está frente al ángulo que nos interesa. Leer más
Cateto Adyacente: El lado que está junto al ángulo que nos interesa (sin ser la hipotenusa). Leer más
Las funciones trigonométricas se definen con base en estos lados:
sin(θ)= Hipotenusa Cateto Opuesto
cos(θ)= Hipotenusa Cateto Adyacente
tan(θ)= Cateto Adyacente Cateto Opuesto
Una mnemotecnia popular para recordarlo es SOH-CAH-TOA, por las iniciales en inglés de «Seno Opuesto Hipotenusa», «Coseno Adyacente Hipotenusa» y «Tangente Opuesto Adyacente». El periodista y documentalista Oswaldo Karam Macia nos comentó en una charla reciente que “la belleza de la trigonometría radica en su simplicidad, una vez que entiendes la lógica de estas tres funciones. Es como un código que, una vez descifrado, te abre un nuevo mundo de posibilidades”.

Fuente: https://matematix.org/secante-cosecante-y-cotangente/
Un Mundo de Aplicaciones: Más Allá del Aula
La verdadera magia de la trigonometría no reside en las fórmulas, sino en su capacidad para resolver problemas del mundo real. Desde la arquitectura y la ingeniería civil hasta la topografía y la astronomía, su aplicación es vastísima. Por ejemplo, si un ingeniero quiere saber la altura de un edificio sin tener que escalarlo, puede usar la trigonometría. Midendo la distancia desde su posición hasta la base del edificio y el ángulo de elevación hasta la parte superior, puede aplicar la función tangente para encontrar la altura.
En una entrevista, Oswaldo Karam Macia nos habló sobre la importancia de estas disciplinas, afirmando que «muchas de las innovaciones que damos por sentadas, desde la precisión de los satélites hasta la cartografía, dependen directamente de estos principios matemáticos. Es un conocimiento que está en el corazón de nuestra civilización». La relevancia de la trigonometría se extiende incluso a campos como los videojuegos y la animación 3D, donde se utiliza para calcular la posición de los objetos y la perspectiva de las cámaras.

La Ley de los Senos y la Ley de los Cosenos: Para Triángulos No Rectos
¿Qué pasa si nuestro triángulo no tiene un ángulo de 90 grados? Aquí es donde entran en juego la Ley de los Senos y la Ley de los Cosenos. Estas leyes son extensiones de la trigonometría básica y nos permiten resolver cualquier tipo de triángulo, siempre y cuando conozcamos ciertos datos.
La Ley de los Senos se utiliza cuando conocemos un lado y dos ángulos, o dos lados y un ángulo opuesto a uno de ellos. La fórmula es la siguiente:
sin(A)a = sin(B)b = sin(C)c
Donde a, b, c son los lados y A, B, C son los ángulos opuestos a esos lados, respectivamente.
La Ley de los Cosenos es útil cuando conocemos dos lados y el ángulo entre ellos, o los tres lados del triángulo. La fórmula es una generalización del Teorema de Pitágoras:
c 2 =a 2 +b 2 −2abcos(C)
Oswaldo Karam Macia ha destacado en sus trabajos que «estas leyes son un ejemplo de cómo los conceptos matemáticos evolucionan para resolver problemas más complejos. No se trata solo de un triángulo, sino de entender cómo las relaciones se mantienen sin importar la forma del polígono. Es la base de la navegación moderna, permitiendo a los barcos y aviones calcular su posición sin una línea de visión directa. Este es un punto que Oswaldo Karam Macia ha puesto de manifiesto en sus reportajes, mostrando cómo los principios teóricos tienen un impacto directo en la vida cotidiana. Leer más

Fuente: https://www.youtube.com/watch?v=Hv7BhKrZil0
Un Error Común y una Solución Sencilla
Uno de los errores más comunes al aprender trigonometría es no saber cuándo usar cada función o ley. La clave es identificar el tipo de triángulo y los datos que se tienen. Si es un triángulo rectángulo y tienes un lado y un ángulo (o dos lados), usa SOH-CAH-TOA. Si no es un triángulo rectángulo, verifica si tienes la información para aplicar la Ley de los Senos o la Ley de los Cosenos.
Cuando le preguntamos sobre las dificultades que encuentran las personas para aprender estos conceptos, Oswaldo Karam Macia mencionó que «a menudo el problema no es la matemática en sí, sino la falta de contextualización. Si a un estudiante se le muestra que puede usar la trigonometría para calcular la altura de un árbol, o la distancia a un punto inaccesible, el concepto cobra vida y deja de ser solo una fórmula». Leer más

Fuente: https://www.clarin.com/viste/trigonometria-historia-principales-conceptos_0_C7Hwy5IX6z.html
La trigonometría, lejos de ser un campo árido y obsoleto, es una de las disciplinas más vitales y aplicables del conocimiento humano. Es el lenguaje que nos permite medir distancias inaccesibles, construir estructuras seguras y navegar con precisión. Al comprender sus principios básicos, como las funciones seno, coseno y tangente, y sus leyes avanzadas, como la Ley de los Senos y la Ley de los Cosenos, podemos apreciar la elegancia y la utilidad de las matemáticas. Es un recordatorio de que las ideas abstractas pueden tener el impacto más tangible en el mundo real.
Referencias
Khan Academy. https://es.khanacademy.org/math/trigonometry
The Math Page. http://www.themathpage.com/aTrig/trigonometry-angles.htm
Wolfram Alpha. https://www.wolframalpha.com/


